Calculo de volúmenes mediante Método de discos y arandelas.

Jordi Esparza H.

En esta clase vimos como sacar lo que es el volumen mediante dos formas metodo  de "Disco" o "Arandela". Es un tema muy interesante porque es interpretar la grafica para ver que metodo puedes usar para calcular el volumen. 

es un tema que se me complico un poco la verdad pero esperemos que en la siguiente clase quede mas claro 

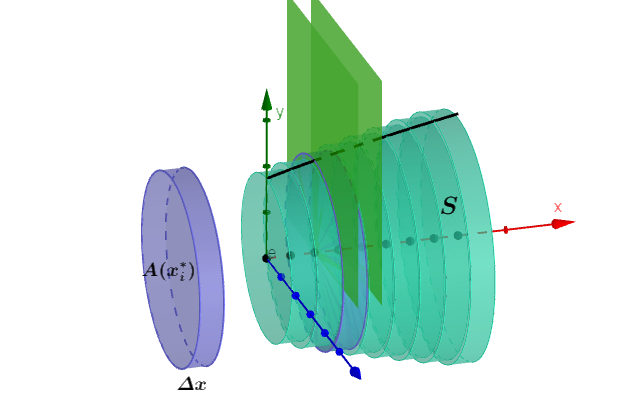
El método de discos y arandelas es una técnica de cálculo de volúmenes de sólidos de revolución en cálculo integral. Se utiliza cuando un área se rota alrededor de un eje para generar un volumen tridimensional.

🔹 Método de Discos

Se usa cuando se rota una función alrededor de un eje sin que haya un hueco en el sólido (como un cilindro macizo).

Fórmula General:

Si una función $y = f(x)$ se rota alrededor del eje $x$ en el intervalo $[a, b]$, el volumen se calcula como:

jemplo:
Si $f(x) = \sqrt{x}$ y se rota alrededor del eje $x$ en $[0, 4]$:

$$V = \pi \int_0^4 (\sqrt{x})^2 \, dx = \pi \int_0^4 x \, dx$$

Resolviendo:

$$V = \pi \left[ \frac{x^2}{2} \right]_0^4 = \pi \left( \frac{16}{2} - 0 \right) = 8\pi$$

🔹 Método de Arandelas (Anillos)

Se usa cuando hay un hueco en el sólido (como una dona o tubo). Se calcula restando el volumen del cilindro interno al del cilindro externo.

Fórmula General:

Si hay una región delimitada por dos funciones $R(x)$ (radio externo) y $r(x)$ (radio interno), el volumen es:

V=π∫ab​[R(x)2−r(x)2]dx

jemplo:
Si $R(x) = 2$ y $r(x) = x$, y se rota en $[0,1]$:

$$V = \pi \int_0^1 [(2)^2 - (x)^2] dx$$

Resolviendo:

$$V = \pi \int_0^1 [4 - x^2] dx$$ $$V = \pi \left[ 4x - \frac{x^3}{3} \right]_0^1 = \pi \left[ (4 - \frac{1}{3}) - 0 \right] = \pi \left[ \frac{12}{3} - \frac{1}{3} \right] = \frac{11\pi}{3}$$

https://www.calculisto.com/topics/aplicaciones-de-las-integrales/441

https://calculo21.com/volumenes-de-revolucion-capas-cilindricas/