Sustitution trigonometrical


Sustitución trigonométrica 

Jordi Esparza H.

En esta clase vimos lo que es la sustitución trigonométrica es un tema bastante interesante ya que al momento de hacer la sustitución se hace un poco extenso para poder encontrar o hacer más pequeña la expresión para poder derivar, en lo personal se me hizo muy enredoso no entendí muy bien pero buscare más videos o ejemplos para poder entenderlo más. 

En matemáticas, la  sustitución trigonométrica  consiste en la sustitución de determinadas expresiones mediante el uso de funciones trigonométricas. En cálculo, la sustitución trigonométrica es una técnica que permite evaluar integrales, puesto que se pueden utilizar identidades trigonométricas para simplificar ciertas integrales que contienen expresiones radicales.

Se hace el cambio de variable   y se utiliza la identidad trigonométrica .   


Ejemplo

Para calcular la integral

se puede realizar el cambio de variable

entonces











Los pasos anteriores requirieron que  y .  

Es posible elegir  para que sea la raíz principal de e imponer la restricción  utilizando la función arco seno  .       

Para una integral definida, se debe averiguar cómo cambian los límites de la integración. Por ejemplo, cuando  va de   a , entonces  va de  a , y  va de  a . En consecuencia,               

Se necesita elegir los límites con cuidado. Debido a que la integración anterior require que , ,  solo puede pasar de  0 a  . Si se ignora esta restricción, se podría haber elegido  para pasar de  a , lo que habría resultado en un valor real negativo.    

Alternativamente, se deben evaluar completamente las integrales indefinidas antes de aplicar las condiciones de contorno. En ese caso, la antiderivada da 




    


como antes.


La  sustitución trigonométrica  es un método de integración. En lugar de sustituir usando una nueva variable que es función de x (u=f(x)), se define ax como una función trigonométrica de una nueva variable (x=f(θ)).

El método consiste en:

  • Reescribir la ecuación en términos de la variable (θ) y su diferencial (dθ)
  • Resolver la integral
  • Reescribir el resultado en términos de x








referencias 

https://cienciayt.com/matematicas/calculo-integral/sustitucion-trigonometrica/

https://es.wikipedia.org/wiki/Integraci%C3%B3n_por_sustituci%C3%B3n_trigonom%C3%A9trica


Ubicación: Ojinaga 26375-1, El Laurel, El Refugio, 22253 Tijuana, B.C., Mexico

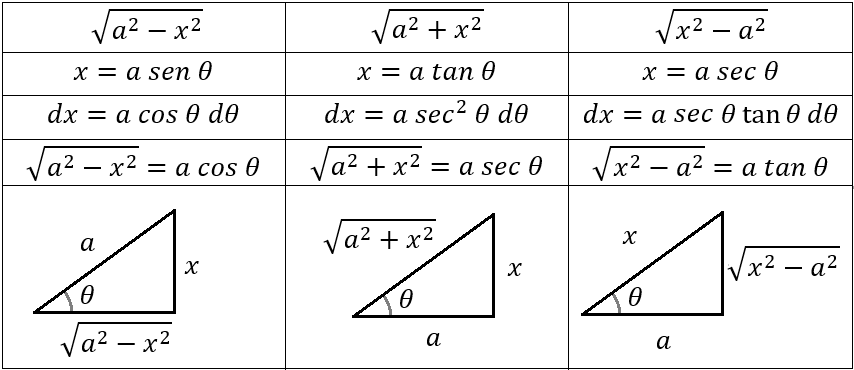
Comentarios

Publicar un comentario

Entradas más populares de este blog

Calculo de volúmenes mediante Método de discos y arandelas.

Imagen
 Calculo de volúmenes mediante Método de discos y arandelas. Jordi Esparza H. En esta clase vimos como sacar lo que es el volumen mediante dos formas metodo  de "Disco" o "Arandela". Es un tema muy interesante porque es interpretar la grafica para ver que metodo puedes usar para calcular el volumen.  es un tema que se me complico un poco la verdad pero esperemos que en la siguiente clase quede mas claro  El método de discos y arandelas es una técnica de cálculo de volúmenes de sólidos de revolución en cálculo integral. Se utiliza cuando un área se rota alrededor de un eje para generar un volumen tridimensional. 🔹 Método de Discos Se usa cuando se rota una función alrededor de un eje sin que haya un hueco en el sólido (como un cilindro macizo). Fórmula General : Si una función y = f ( x ) y = f(x) y = f ( x ) se rota alrededor del eje x x x en el intervalo [ a , b ] [a, b] [ a , b ] , el volumen se calcula como: jemplo : Si f ( x ) = x f(x) = \sqrt{x} f ( x ) = x...
Leer más

Reglas de derivación Trigonométricas

Imagen
  Reglas de derivación Trigonométricas en esta clase empezamos aver las reglas de la derivacion trigonometricas practicamente se podria decir que es lo mismo que las reglas de la derivacion normales porque se siguen usando, Es un tema un tanto mas complejo por el hecho de empezar a ver SENO,COSENO,TANGENTE y esos terminos que al principo uno no tiene conocimiento de ellos pero entendiendo y llevando la relacion con las demas reglas se entiende bien obviamente con su complejidad del tema claro. La derivación de funciones trigonométricas se resume en unas reglas muy sencillas de recordar. En esencia, la derivada del seno es igual al coseno, y la del coseno coincide con el seno cambiado de signo (todo ello multiplicado, claro está, por la derivada de la función que figura como argumento de la razón trigonométrica).  Las restantes funciones trigonométricas se determinan aplicando las reglas de la derivación de un cociente de funciones (para la tangente, la cotangente, etcétera) ...
Leer más