Integrales Indefinidas

 Integrales Indefinidas

JORDI ESPARZA H.

En esta clase comenzamos a estudiar el concepto de integrales en cálculo, así como sus reglas y aplicaciones. En lo personal, me resultó un tema accesible, ya que en el curso anterior adquirimos un conocimiento general sobre derivadas, y ambos procesos presentan ciertas similitudes.

Las primeras cinco reglas que analizamos en clase me parecieron sencillas, especialmente porque, como mencionó el profesor, en muchas situaciones es posible regresar a la regla número dos. Además, he comenzado a interesarme más en las derivadas, ya que encuentro su estudio y aplicación bastante entretenidos.

QUE SON LA INTEGRACION?

La integración es un concepto fundamental del cálculo y del análisis matemático. Básicamente, una integral es una generalización de la suma de infinitos sumandos, infinitesimalmente pequeños: una suma continua. La integral es la operación inversa al diferencial de una función.

El cálculo integral, encuadrado en el cálculo infinitesimal, es una rama de las matemáticas en el proceso de integración o anti derivación. Es muy común en la ingeniería y en la ciencia; se utiliza principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de revolución.

Siguiendo a Leibniz, a veces usaremos el término integral indefinida en lugar de antiderivada. Antiderivar también es integrar. En el símbolo se denomina signo de integral y f(x) se llama integrando. Así, integramos el integrando y de este modo evaluamos la integral indefinida. Tal vez Leibniz utilizó el adjetivo indefinida para sugerir que la integral indefinida siempre incluye una constante arbitraria.



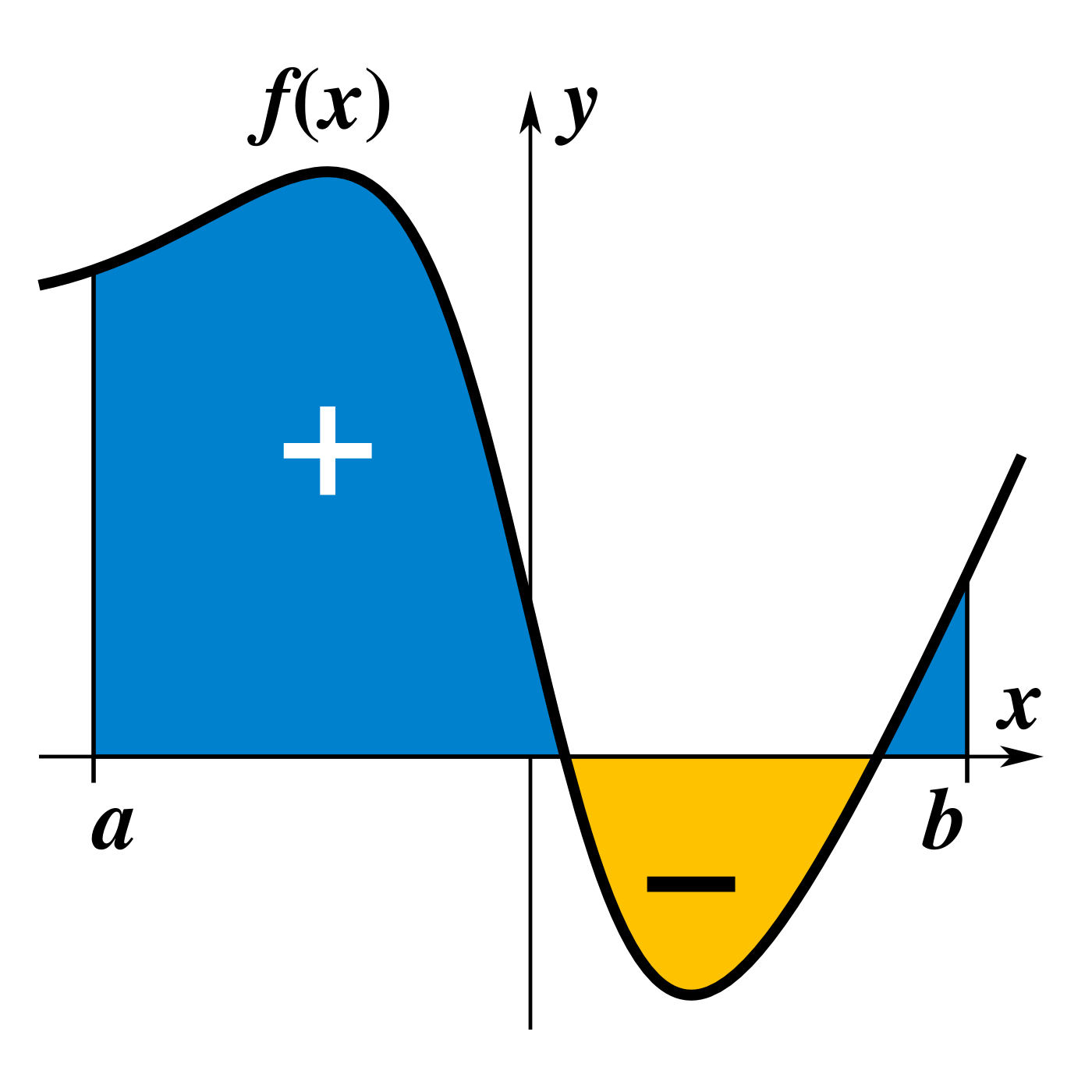
La integral definida de una función representa el área limitada por la gráfica de la función, en un sistema de coordenadas cartesianas con signo positivo cuando la función toma valores positivos y signo negativo cuando toma valores negativos.


Al calcular una integral, es fundamental seguir una serie de reglas que nos permiten resolverla de manera correcta y eficiente. Estas reglas establecen los procedimientos adecuados para aplicar la integración a distintas funciones, facilitando la obtención de resultados precisos. A lo largo del proceso, es importante identificar qué regla utilizar en cada caso, ya que algunas integrales pueden resolverse directamente, mientras que otras requieren transformaciones o técnicas adicionales. El correcto dominio de estas reglas es esencial para comprender y aplicar la integración en diversos contextos matemáticos y científicos.



videos:


VIDEO 1 



VIDEO 2 


FUENTES 

https://es.wikipedia.org/wiki/Integraci%C3%B3n
https://www.notefleet.com/notes/125/formulas-basicas-de-calculo-integral
LIBRO DE CALCULO DIFERENCIAL Y INTEGRAL 

videos 
https://www.youtube.com/watch?v=9s_ICZNINhY
https://www.youtube.com/watch?v=76LARwCxtHw


















Comentarios

Publicar un comentario

Entradas más populares de este blog

Calculo de volúmenes mediante Método de discos y arandelas.

Imagen
 Calculo de volúmenes mediante Método de discos y arandelas. Jordi Esparza H. En esta clase vimos como sacar lo que es el volumen mediante dos formas metodo  de "Disco" o "Arandela". Es un tema muy interesante porque es interpretar la grafica para ver que metodo puedes usar para calcular el volumen.  es un tema que se me complico un poco la verdad pero esperemos que en la siguiente clase quede mas claro  El método de discos y arandelas es una técnica de cálculo de volúmenes de sólidos de revolución en cálculo integral. Se utiliza cuando un área se rota alrededor de un eje para generar un volumen tridimensional. 🔹 Método de Discos Se usa cuando se rota una función alrededor de un eje sin que haya un hueco en el sólido (como un cilindro macizo). Fórmula General : Si una función y = f ( x ) y = f(x) y = f ( x ) se rota alrededor del eje x x x en el intervalo [ a , b ] [a, b] [ a , b ] , el volumen se calcula como: jemplo : Si f ( x ) = x f(x) = \sqrt{x} f ( x ) = x...
Leer más

Reglas de derivación Trigonométricas

Imagen
  Reglas de derivación Trigonométricas en esta clase empezamos aver las reglas de la derivacion trigonometricas practicamente se podria decir que es lo mismo que las reglas de la derivacion normales porque se siguen usando, Es un tema un tanto mas complejo por el hecho de empezar a ver SENO,COSENO,TANGENTE y esos terminos que al principo uno no tiene conocimiento de ellos pero entendiendo y llevando la relacion con las demas reglas se entiende bien obviamente con su complejidad del tema claro. La derivación de funciones trigonométricas se resume en unas reglas muy sencillas de recordar. En esencia, la derivada del seno es igual al coseno, y la del coseno coincide con el seno cambiado de signo (todo ello multiplicado, claro está, por la derivada de la función que figura como argumento de la razón trigonométrica).  Las restantes funciones trigonométricas se determinan aplicando las reglas de la derivación de un cociente de funciones (para la tangente, la cotangente, etcétera) ...
Leer más

Sustitution trigonometrical

Imagen
Sustitución trigonométrica  Jordi Esparza H. En esta clase vimos lo que es la sustitución trigonométrica es un tema bastante interesante ya que al momento de hacer la sustitución se hace un poco extenso para poder encontrar o hacer más pequeña la expresión para poder derivar, en lo personal se me hizo muy enredoso no entendí muy bien pero buscare más videos o ejemplos para poder entenderlo más.  En matemáticas, la  sustitución trigonométrica  consiste en la sustitución de determinadas expresiones mediante el uso de funciones trigonométricas. En cálculo, la sustitución trigonométrica es una técnica que permite evaluar integrales, puesto que se pueden utilizar identidades trigonométricas para simplificar ciertas integrales que contienen expresiones radicales. Se hace el cambio de variable    y se utiliza la identidad trigonométrica . incógnita = a señor ⁡ θ       señor 2 ⁡ ( θ ) + porque 2 ⁡ ( θ ) = 1 Ejemplo Para calcular la integral ∫ ...
Leer más